算法笔记：算法复杂度分析

什么是算法复杂度？

维基百科：In computer science, the analysis of algorithms is the determination of the computational complexity of algorithms, that is the amount of time, storage and/or other resources necessary to execute them.

算法复杂度，就是计算机程序在运行时，消耗的时间资源与空间资源的多少。

算法复杂度分为时间复杂度与空间复杂度。

时间复杂度

1. 时间复杂度简介

时间复杂度，简单来说，就是一段程序执行的时间长短。但是在实际应用中，我们很难准确的计算出准确的执行时间，因为影响具体程序执行时间的因素太多：硬件（CPU，内存，寄存器），软件（编译器，垃圾回收机制），系统（网络，操作系统）。准确计算算法运行的时间也没有必要，我们只需要知道，相对的，哪个算法花费时间少，哪个算法花费时间多就够了。

我们知道，一个算法花费的时间是与其需要执行的语句成正比例的，因此衡量算法复杂度，我们只需要衡量语句的执行次数。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

2. 时间复杂度基本知识

（1）log-log plot

在算法时间复杂度分析中，我们常用log-log plot去衡量时间复杂度，即横坐标为logN(N为问题规模)，纵坐标为logT(T为时间频度)

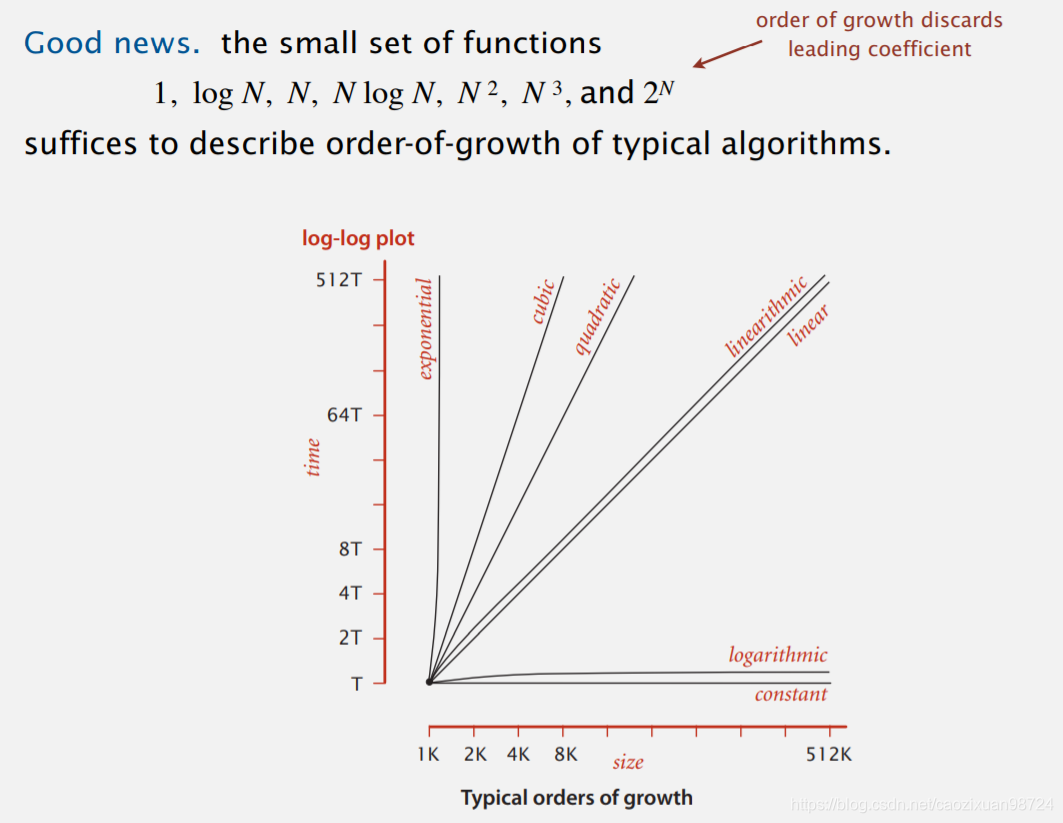
exponential:指数型复杂度

cubic:N^3

linearithmic:NlogN

linear:N

logarithmic:logN

constant:c

quadratic:N^2

在log-log plot中，通过斜率，我们可以直观的感受到算法的时间复杂度。

（2）符号表示

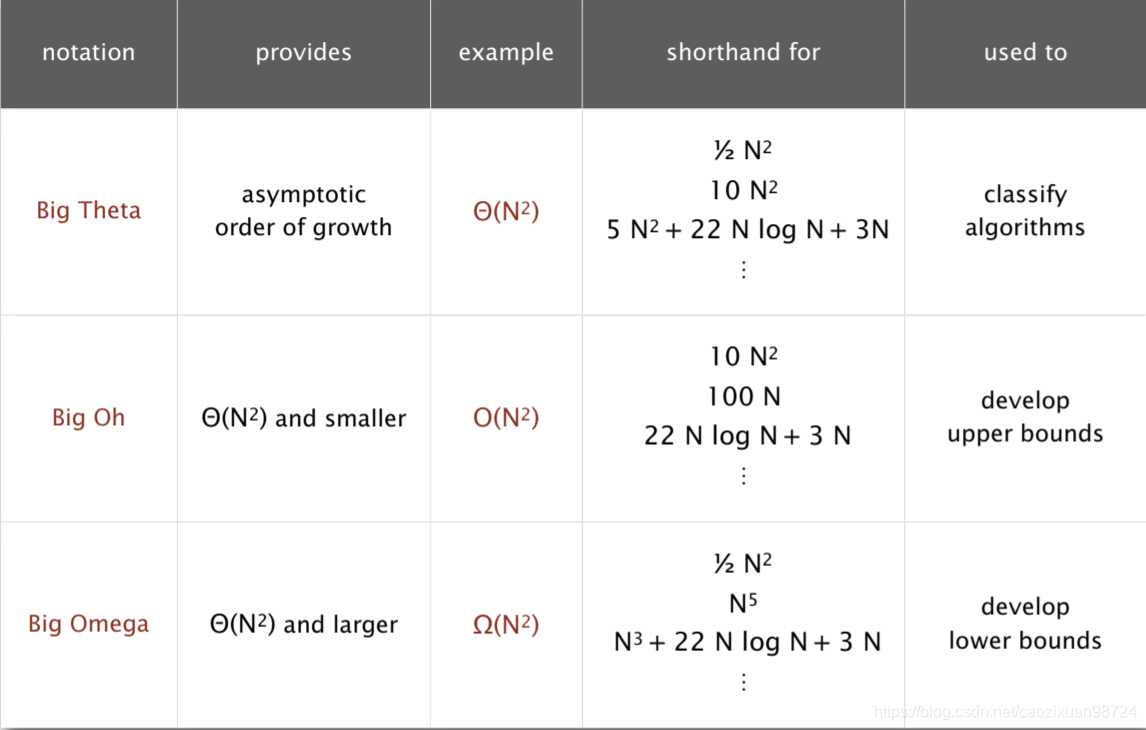
稍微要注意一些这几个符号的区别。

θ(N^2)代表时间复杂度渐进相等。

O(N^2)代表时间复杂度小于等于N^2这个量级。

Ω(N^2)代表时间复杂度大于等于N^2这个量级。

（3）不同的情况

3. 时间复杂度分析

算法复杂度分析在这里给出两个例子。

（1）矩阵相乘

这个例子来自百度百科：算法复杂度，详情可参考原文。

# define n 100 // n 可根据需要定义,这里假定为100void MatrixMultiply(int A[n][n]，int B [n][n]，int C[n][n]){ //右边列为各语句的频度    int i ,j ,k;    for(i=0; i<n;i++) //n    for (j=0;j<n;j++) { //n*n        C[i][j]=0; //n²        for (k=0; k<n; k++) //n²*n        C[i][j]=C[i][j]+A[i][k]*B[k][j];//n³    }}

该算法中所有语句的频度之和(即算法的时间耗费)为：

T(n)=2n^3+3n^2+2n+1

分析：

语句(1)的循环控制变量i要增加到n，测试到i=n成立才会终止。故它的频度是n+1。但是它的循环体却只能执行n次。语句(2)作为语句(1)循环体内的语句应该执行n次，但语句(2)本身要执行n+1次，所以语句(2)的频度是n(n+1)。同理可得语句(3)，(4)和(5)的频度分别是n2，n2(n+1)和n3。

算法MatrixMultiply的时间耗费T(n)是矩阵阶数n的函数。

（2）二分搜索

public static int binarySearch(int[] a, int key) { int lo = 0, hi = a.length-1; while (lo <= hi) { int mid = lo + (hi - lo) / 2; if (key < a[mid]) hi = mid - 1; else if (key > a[mid]) lo = mid + 1; else return mid; } return -1; }

在有序数组中，我们最多比较1 + lg N次即可得到最终的结果。

4. 递归程序的时间复杂度

递归程序的时间复杂度是一个相对复杂的问题。

一般情况下，算法中基本操作重复的次数就是问题规模n的某个函数f（n），进而分析f（n）随n的变化情况并确定T（n）的数量级。这里用‘o’来表示数量级，给出算法时间复杂度。 T（n）=o（f（n））；它表示随问题规模n的增大，算法的执行时间增长率和f（n）增长率成正比，这称作算法的渐进时间复杂度。而我们一般情况下讨论的最坏的时间复杂度。

对于递归程序的时间复杂度，我们很难直观的计算出来，很多时候需要用到一些数学手段求解，具体信息可以参考这篇博文递归算法时间复杂度分析。