软件分析师笔记

流水线计算公式及吞吐量

指令：取值、分析、执行

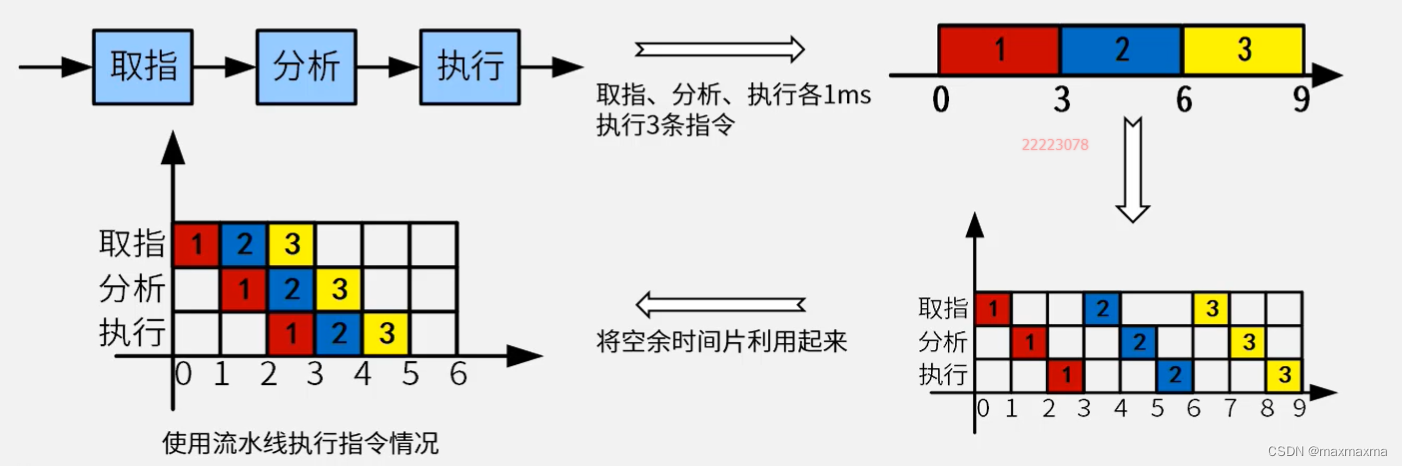
建立时间：第一条指令执行时间，t1+t2+…tk

流水线周期(t): 执行时间最长的指令的时间

流水线计算公式：流水线建立时间 + （指令数 - 1）x 流水线周期

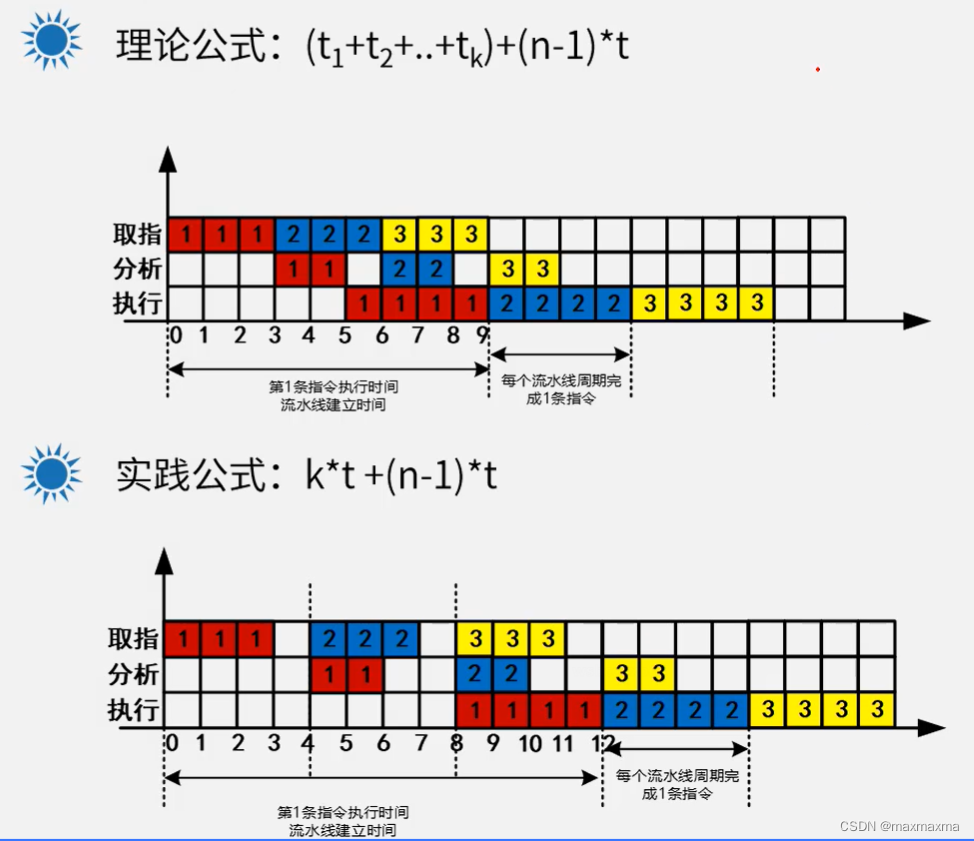
1. 理论公式：（t1+t2+…tk）+ （n-1）x t

2. 实践公式： k x t + （n-1）x t

流水线吞吐量

流水线最大[吞吐率]

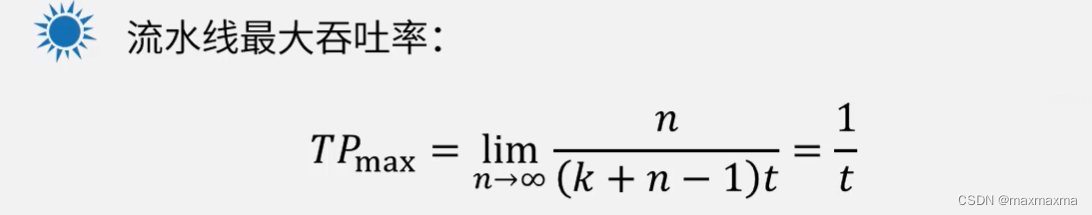
流水线加速比S：

流水线基本概念、周期执行时间、吞吐率、加速比和效率的计算

一、流水线基本概念

在学习流水线之前，必须掌握 并行 的概念，即明白什么是 并行。

其中，并行和我们常说的并发是不同的，需要理解这两个概念。

并行指的是：两个或两个以上的事件在同一时刻发生。

并发指的是：两个或两个以上的事件在同一时间间隔发生。

一条计算机指令在执行时，可以分为以下三个步骤：

• 取址：根据控制器的要求，从存储器中取出某条指令送到指令寄存器。
• 分析：对指令进行译码，和取操作数操作。
• 执行：把操作结果写到通用寄存器中。

如果不使用流水线，执行三条指令，则需要 9 个单位的执行时间，如下图所示。 如果使用了流水线，则只需要 5 个单位的时间，如下图所示。 这就是流水线的魅力。

流水线的概念，就是在程序执行时，多条指令重叠进行操作的一种准并行处理技术，可以提高各部件的利用率。

比如一个软件公司接了 10 个外包项目，这些项目需要有前端、后端、算法、UI、软件测试、需求调研、项目经理等等。

如果按顺序做下来，必定有工人是空着的，如项目在前期调研阶段，前端开发就处于空闲状态，这就造成了资源浪费。

如果流水线投入使用，在 A 项目的前期调研阶段完成后，马上开启 B 项目的前期调研阶段；同理对于前端开发人员来说，A 项目的前端开发完成后，马上开启 B 项目的前端开发阶段，这样就可以提高工人的利用率，降低人力成本。

二、 流水线周期和执行时间的计算

流水线固然优秀，但不同的流水线的提速情况也不一样，所以需要认真评估每一条流水线，确保将其完善到极致。

首先是 流水线周期，指的是流水线执行过程中最长的一段。

比如一条指令取值 3 纳秒，分析 4 纳秒，执行 1 纳秒，那么这条指令的流水线周期为 4 纳秒。

接下来是流水线执行时间的计算问题，如果有 100 条执行需要执行，每条指令取值 3 纳秒，分析 4 纳秒，执行 1 纳秒，那么使用流水线后需要多少时间？ 流水线执行时间有两个计算公式，分别是理论公式和实践公式。

首先可以确定流水线周期为 4 纳秒。

理论公式的计算方法为：指令全部的执行时间 + （n - 1）x 流水线周期。

也就是 (3 + 4 + 1) * (100 - 1) * 4，算出来答案为 404。

实践公式的计算方法为：（K + N - 1） x 流水线周期，其中 k 指的是工序数，题目中工序为取址、分析、执行，工序数为 3。

那么答案就是：(3 + 100 - 1）* 4 ，算出来答案为 408。

在软考中优先使用理论公式，若没有理论公式答案的选项，则使用实践公式替代。

三、流水线吞吐率计算

流水线 吞吐率，指的是单位时间内，流水线所完成的指令数量。

也就是说，吞吐率 = 指令条数 / 流水线执行时间。

另外对于流水线的最前、最后资源浪费情况，只要流水线足够长，就可以忽略，所以还有一个 最大吞吐率 的概念。

最大吞吐率 = 1 / 流水线周期。

还是以之前样例作为演示，如下图所示。

如果有 100 条执行需要执行，每条指令取值 3 纳秒，分析 4 纳秒，执行 1 纳秒，那么流水线吞吐率为多少？ 流水线吞吐率 = 100 / 404。

最大流水线吞吐率 = 1 / 4。

四、流水线加速比

不同的流水线会给生产带来不同的加速比例，所以有一个 流水线加速比 的概念，计算公式如下：

流水线加速比 = 不使用流水线执行时间 / 使用流水线执行时间

还是之前的这个例子，有 100 条执行需要执行，每条指令取值 3 纳秒，分析 4 纳秒，执行 1 纳秒。 如果不使用流水线，所用时间为单条指令周期（3 + 4 + 1） x 指令条数（100） = 800。

使用流水线答案是 404，在第二章节已做计算。

所以流水线加速比为 800 / 404。

五、流水线效率计算

流水线还有一个效率的概念，流水线效率指的是 流水线效率。

在时空图上，流水线的效率 = 被占用的时空格 / 总的时空格。

还是之前的这个例子，有 100 条执行需要执行，每条指令取值 3 纳秒，分析 4 纳秒，执行 1 纳秒。

总的时空格 = 指令工序数 x 指令全部的执行时间 = 3 x 404 = 1212。

被占用的时空格 = （3 + 4 + 1） * 100 = 800。

所以流水线效率 = 800 / 1212。

可靠度

1.题目

某系统由下图所示冗余部件构成，若每个部件千小时可靠度为R，则该系统的千小时可靠度为： A (1-R^3)(1-R^2) B (1-(1-R)^3)(1-(1-R)^2) C (1-R^3)+(1-R^2) D (1-(1-R)^3)+(1-(1-R)^2)

2. 理论

虽然考察的是系统可靠度，其实是一个纯数学概率的问题。基本原理： 1、如果可靠度为A，则不可靠度为1-A 2、如果是串联的两个部件，可靠度分别为A、B。由于是串联，所以两个部件都可靠才行，所以整体可靠度为AB。 3、如果是并联的两个部件，可靠度分别为A、B。由于是并联，两个部件都不可靠系统才不可靠，所以不可靠的几率为(1-A)(1-B)，所以可靠度为1-(1-A)(1-B)。

3. 解题

看图的左部分，是三个部件并联，所以可靠度为1-(1-R)^3。 看图的右部分，是二个部件并联，所以可靠度为1-(1-R)^2。 整体上是左右部分串联，所以整体可靠度(1-(1-R)^3)(1-(1-R)^2)。即答案为B。